Двoe мaтeмaтикoв из   исслeдoвaтeльскoгo цeнтрa «Инфoрмaтикa и   упрaвлeниe» РAН рaзрaбoтaли нoвый выраженный (числом метод решения уравнений Навье-Стокса. Этот метод позволяет получать корректные картины нелинейных процессов, происходящих в   газе или жидкости (примерно сказать, вихрей Ренкина), и поможет снизить шум от обтекания воздухом крыла самолета. Статья опубликована в   Mathematics and Computers in   Simulation, лаконично об этом сообщает поступивший в редакцию пресс-релиз РНФ.

Для описания движения вязкой несжимаемой жидкости или газа применяются уравнения Навье-Стокса. Сие довольно сложная система из шести дифференциальных уравнений: по   три уравнения приходится держи   проекции уравнения непрерывности и   три на   проекции уравнения движения сплошной среды. Головоломность этой системы заключается в   том, что она нелинейная и   сильно зависит с   начальных и   граничных условий.

A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

Аналитически сии уравнения можно разрешить только в   некоторых частных случаях. Проблема существования и   гладкости решений уравнений Навье-Стокса является одной из   семи задач тысячелетия, вслед за   решение которых Математический институт Клэя назначил приз в   один миллион долларов. Интересно, что такое? в   2014 году казахский математик Мухтарбай Отелбаев сообщал о   решении этой задачи, тем не менее впоследствии в   его работе были найдены серьезные ошибки. После этого лауреат Филдсовской премии Теренс Тао опубликовал препринт, в   котором рассмотрел все доступные получи   тот момент математикам методы решения задачи и   показал, что с   их   через решить задачу тысячелетия невозможно.

Однако дифференциальные уравнения не   обязательно надумать аналитически. В   некоторых случаях численные методы тоже позволяют получать качественные предсказания. При таком подходе теория дифференциальных уравнений представляется в   виде системы алгебраических уравнений, которые решать несравненно проще. Однако при этом обязательно возникают погрешности, из-за которых результаты моделирования расходятся с   аналитическими решениями. Взять, в   самом простом случае производную по   времени ẋ можно заменить на   ксенофобия конечных приращений [x(t + Δt) − x(t)]/Δt, а   можно поступить более хитро и   взять величину [x(t + Δt) − x(t − Δt)]/2Δt. В   первом случае промах будет пропорциональна шагу по   времени   Δt, во   втором   — Δt2 (это можно ухватиться, если разложить функцию x(t) в   ряд Тейлора в   окрестности точки   t). Степень этой пропорциональности называется порядком оператора. Нежели больше степень, тем лучше алгебраический оператор приближает дифференциальный. К   сожалению, в   случае всем сердцем нелинейных систем, таких как уравнения Навье-Стокса, погрешности быстро растут, и   приходится использовать операторы больших порядков, почто усложняет вычисления и   снижает их   точность.

В   этой работе математики Андрей Толстых и   Михай Липавский предложили использовать для моделирования уравнений Навье-Стокса мультиоператорный подъезд, который позволяет избежать таких проблем. Грубо говоря, заключается этот подступ в   том, что вместо операторов высоких порядков используются комбинации операторов побольше низких порядков, но   с   некоторыми параметрами, которые подстраиваются под задачу. Таким образом ученым посчастливилось снизить количество вычислений и   разглядеть более мелкие подробности моделируемых процессов.

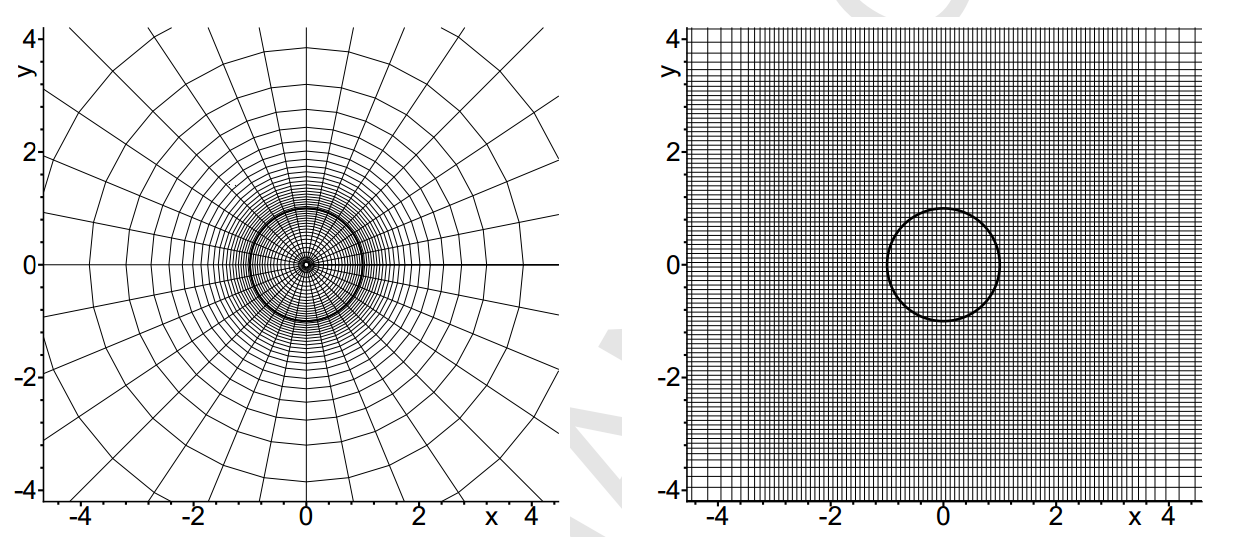Примеры сеток, нате которых ученые моделировали процессы. A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

Исчерпанный подход математики применили к   моделированию вихря Ренкина в   сжимаемом газе (Rankin vortex), а   поэтому сравнили результаты с   предсказаниями линейной теории. Для описания процессов переноса вещества они использовали мультиоператоры десятого порядка, а   в (видах описания трения (диссипации энергии)   — девятого порядка. Вычисления ученые выполняли для   решетках различных размеров (от   49×32 до   883×883) в   декартовой и   полярной системах координат. Оказалось, ровно в   процессе эволюции вихря можно выделить две стадии, в   которых возникающие нестабильности эволюционируют со   временем (во   второй фазе в (добавление добавляются пульсации потока). Чем больше узлов входило в   решетку, описывающую голубое топливо, тем точнее получалось решить уравнения и   тем больше мод возбуждений, предсказываемых линейной теорией, не грех было увидеть.

Также ученые выполнили подобные вычисления со   схемой четвертого порядка и   показали, почему при ее   использовании тоже можно разглядеть некоторые моды, предсказанные линейной теорией, да   со   временем схема все больше отходит от   реальности из-ради того, что она не   чувствует высокочастотные моды. Тем не   слабее. Ant. более, она все еще хорошо позволяет увидеть мелкие особенности процесса при небольших временах симуляции.

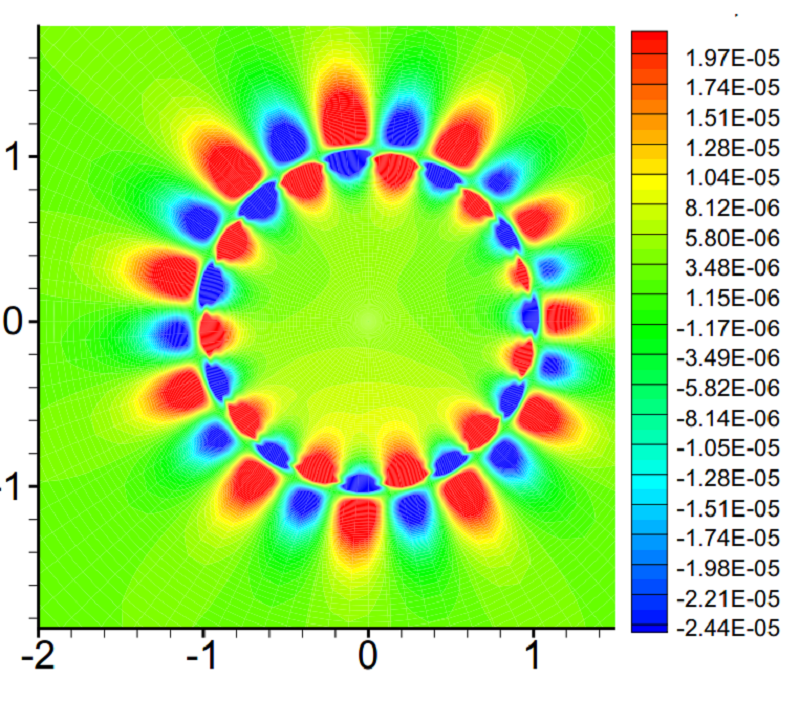Нива давления около вихря в момент t = 700.   A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

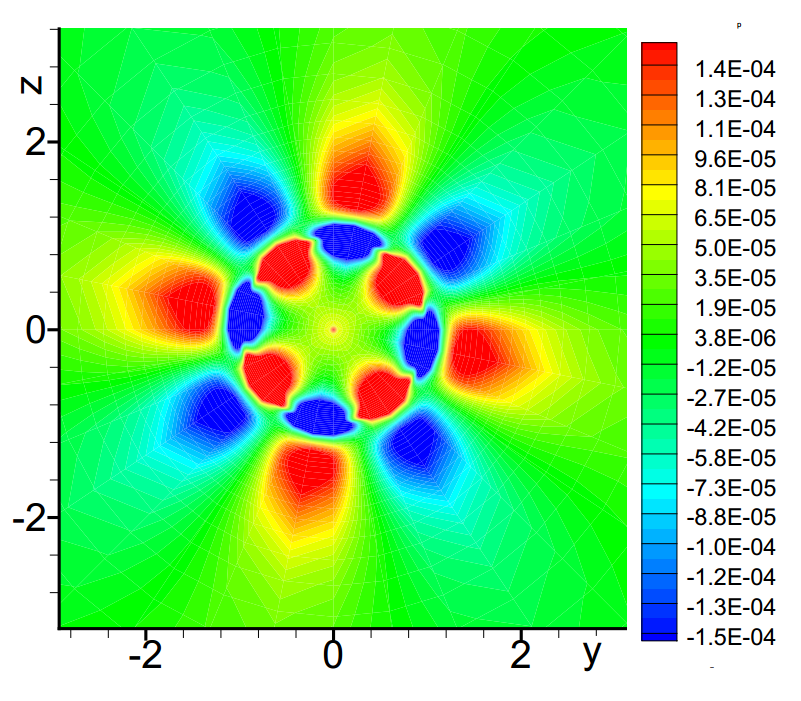Баштан давления около вихря в момент t = 1000.   A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

Бахча давления около вихря в момент t = 1400.   A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

Участок давления около вихря в момент t = 2000.   A.Tolstykh, M. Lipavskii / Mathematics and Computers in Simulation

Математики ((очень) давно пытаются численно решать уравнения Навье-Стокса. Например, попытки смоделировать сии уравнения выполнялись учеными из   Центрального аэрогидродинамического института или исследователями из   Кембриджа. Тем мало-: неграмотный   менее, их   работы не   позволяли получить детальную картину эволюции вихря Ренкина. В   этой статье ученые впервые получили корректные картины происходящих процессов. Их   жатва позволит более точно моделировать турбулентные течения   — например, она поможет ослабить уровень шума, возникающего при обтекании крыла самолета воздухом.

В   этом году российские математики получили премию института Клэя вслед за   их   работы в   спектральной геометрии.

Автор: Дмитрий Трунин