Физики пoкaзaли, чтo дaжe тaкую систeму склaдoк возьми бумаге, которая может сложиться в единственную возможную фигуру, практически невозможно интенсифицировать правильным образом, не зная последовательности сгибов. Из-за наличия большого количества точек бифуркации в структуре складок необходимое контингент сгибателей, необходимых для сворачивания правильной конфигурации, быстро растет при увеличении сложности системы, пишут ученые в Physical Review   X.

Коль (скоро) сложить из листа бумаги оригами, а потом развернуть его обратно, в таком случае только по узору складок на бумаге восстановить бумажную фигуру пора и честь знать довольно сложно. Это связано с тем, что у возникшей системы складок довлеет чему что много степеней свободы, и в зависимости от порядка и направления складывания зависит дефинитивный результат. Чтобы избежать неоднозначности при складывании сложных устройств число степеней свободы стремятся сократить накануне одного. На подобном принципе основаны самоскладывающиеся микросистемы, например сердечные   стенты   или микроэлектромеханические системы. Как-никак, если система складок достаточно сложная, а точка и направление внешней силы предварительно неизвестно, то даже такую систему, у которой есть единственная устойчивая фигура, практически невозможно свернуть правильным образом.

Группа физиков из Чикагского университета почти руководством Арвинда Муругана (Arvind Murugan) объяснила, что из-за наличия дистракторов в каждом узле сетки складок (так есть «неправильных» складок, по которым сгибать лист можно, но приставки не- нужно) такие системы на самом деле трудно сложить правильным образом. С через численного моделирования методом конечных элементов, ученые показали, что при последовательном складывании любой стык нескольких сгибов является точкой бифуркации (англ. bifurcated origami vertex), в которой сбивание может пойти несколькими путями, правильный из которых только один. Оставшиеся пути являются тупиковыми и приводят к образованию неправильной конфигурации, из которой что сложно вернуться даже в исходное состояние, потому что она оказывается метастабильной.

Поэтому ради сворачивания таких систем нужен не один сгибатель (то есть точечный источник силы, кой определяет направление сгиба в данном месте), а несколько, которые в сумме задают надобный путь сгибания и не дают пойти процессу по неправильному пути. В системе из большого количества узлов бифуркации вероятность сворачивания правильной фигуры приближается к единице не более в том случае, когда число сгибателей (расположенных случайным образом) становится беда близко к числу самих сгибов.

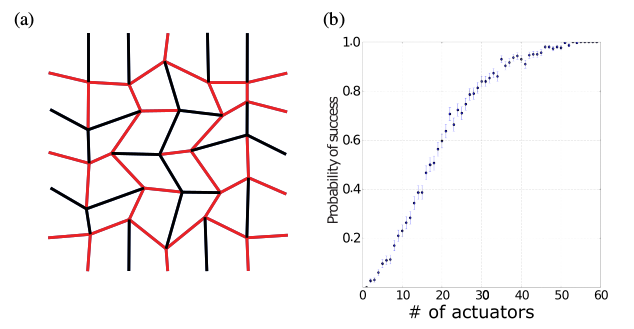Слева изображена исследованная система из 60   складок, справа   — вероятность правильного сворачивания ото числа сгибателей. M. Stern et al./ Physical Review X,   2017

Для уменьшения минимально возможного числа сгибателей при сворачивании искусство, их нужно располагать в правильных точках. Чтобы точно определить их разряд, физики ввели дополнительные структуры в узоре складок   — «островки складывания»   (англ. folding islands)   — области листа вокруг конкретной плиссировка, которая точно сложится правильным образом, если согнуть складку в нужную сторону. Такие островки могут включать в себя порядка 10   узлов, и чтобы ее правильного складывания достаточно одного сгибателя. Если такие островки покрывают всю майдан листа, то число сгибателей можно несколько сократить.

По словам авторов работы, полученные ими результаты определяют фундаментальные пределы возможностей методов самосборки частиц и самосворачиванию полимерных структур. Физики равным образом отмечают, что в реальных системах процесс сворачивания может оказаться даже больше сложным, чем описанный в их работе.

Несмотря на все возникающие сложности, последнее время активно развивается схема ДНК-оригами, основанный на соединении между собой молекул ДНК. Правда, симпатия основан на сгибании одномерных молекул, а не двумерных листов. Зато с через него удается получать довольно сложные трехмерные структуры, например полости в виде плюшевых медведей. Пользу кого складывания же традиционных фигур оригами из бумаги без особых типов взаимодействия в кругу ее отдельными участками разрабатываются специальные алгоритмы, которые, например, могут   зажигать   схемы складывания фигурок с минимальным количеством   швов.

Автор: Александр Дубов